An anecdote:
Track geometry exam, somewhere at a Civil Engineering University.
One of the exam subjects is realignment methods and types of versines.
This important subject was covered during the track course hours but also in four seminars and in a realignment project homework – so it was supposed to be an easy one …
After checking the exam paper, the professor is asking one of the students:
Professor: Give me an example of an usual versine value for railway track alignment!?
Student: … 28…!?
Professor: 28 … what?
Student: 28 … metres?
… Easy, but not easy for everyone.
————————————————
One of the historical methods to survey a track alignment is to measure the offsets from a chord to the running edge of the rail at the centres of successive overlapping chords, laid out along the outer or high rail of the surveyed track (Cope – 1998). These offsets are called versines. This method of surveying the track is sometimes called Hallade survey. The versines are used in the realignment process which consists in smoothing these versines and obtaining a new set of versines and the required slews, to which the track is then set.
The computation of the versines can be done using different methods. If the computation is focused only on smoothing the versine values, keeping the design geometry as close to the existing as possible, the computation process is called rectification.
If the computation is focused on producing an improved alignment, by changing the radius or/and the transition lengths, it is called realignment. (Radu – 1999).
The rectification methods are simpler and can be used and applied easily and sometimes can be used to realign the track through a long iterative process.
The most well-known versine adjustment method is the Hallade rectification method.
All the rectification and realignment methods are based on the direct relation between the versine and the radius.
The versine measured at the middle point of the chord

Figure 1. The versine measured at the chord mid-point
In the right triangle ABC, if we apply the geometric mean theorem, we have:

The versine, v, in track design is very small compared to the radius R. Hence its square value is a small quantity of second order and can be ignored in the equation. This gives us the classic formula of the versine:

For all the railway track applications the chord length is significantly smaller compared to the radius and the approximation mentioned above does not produce any measurable errors.
When the chord length is getting closer to the radius value (c > 30% R) a more precise formula is needed. One way to get this formula is from the right triangle BDO.
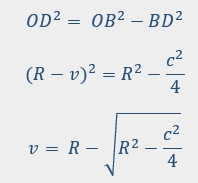
But this later formula is only a theoretical one and if we compare it to the formula we all know, we will find a change in versine insignificant for practical purposes.
The versine measured at an aleatory point on the chord

Figure 2. The versine measured away from the mid-point of the chord
If the versine is not measured at the middle point of the chord, a different formula is required.
In figure 2, for the inscribed quadrilateral ABCE, the angles ∠ABE and ∠ACE are equal.
Expressing the tangent of these angles, we have:

Due to the significant dimensional difference between the radius and the chord, DC is considered equal to (2R-v). This is producing the following equations:

As before, the squared value of v, a small quantity of second order, can be considered null.
Hence, the formula of the versine measured at an aleatory point D on a chord is:

This formula is used in the electronic computation of the tamper corrections and adjustment values in the four point or three point lining method (Lichtberger – 2005, Radu et al. – 2001)
References:
Cope, Geoffrey H. (1993) British railway track: design, construction and maintenance. Permanent Way Institution.
Lichtberger, Bernhard (2005) Track compendium. Eurailpress Tetzlaff-Hestra GmbH & Co. KG, Hamburg
Radu, Constantin (1999) Cai Ferate – Suprastructura Caii (Railway – Track Superstructure) – Course notes. Faculty of Railways, Roads and Bridges – Technical University of Civil Engineering Bucharest
Radu, Constantin (2003) Rectificarea si retrasarea curbelor de cale ferata (Rectification and realignment of the railway track curves). Course notes. Technical University of Civil Engineering Bucharest.
Radu, Constantin; Ungureanu, Valentin Vasile; Ciobanu, Constantin (2001) Determination of the versine corrections and adjustment values. Technical Bulletin – Technical University of Civil Engineering Bucharest


